JMT (Java Modelling Tools) is an integrated environment for performance evaluation, capacity planning and workload characterization of computer and communication systems [1]. A number of cutting-edge algorithms are available for exact, approximate and asymptotic analysis of queueing networks (QNs), with either product-form or non-product-form solutions. Users can define and solve models through a well-designed graphical interface, or optionally an alphanumeric wizard. Released under GPLv2, JMT benefits a large community of thousands of students, researchers and practitioners, with more than 5,000 downloads per year.
The focus of JMT is particularly on QNs, in which jobs travel through a number of stations demanding a certain amount of service at each and possibly suffering a queueing delay due to service contention. Although QNs are a prevailing class of formalisms for performance modeling purposes, they are not suitable for describing systems that exhibit logical behavior (e.g. synchronization). JMT integrates a discrete-event simulator known as JSIM. Inspired by the DICE project, an extension has been contributed to JSIM for supporting Petri nets (PNs), another important class of performance modeling formalisms which are found especially useful for capturing the logical behavior of a system.
Two novel types of stations, Place and Transition, have been designed and implemented in JSIM for simulating PN models. With these stations, JSIM well supports almost all the canonical types of PNs including GSPNs (Generalized Stochastic Petri Nets), CPNs (Colored Petri Nets) and QPNs (Queueing Petri Nets) [2]. High compatibility has been achieved between PN and QN stations. Thus, hybrid models comprising both PN and QN components can also be simulated with JSIM. In hybrid models, PN components are used to exactly depict logical behavior while QN components provide concise representation of queueing behavior.
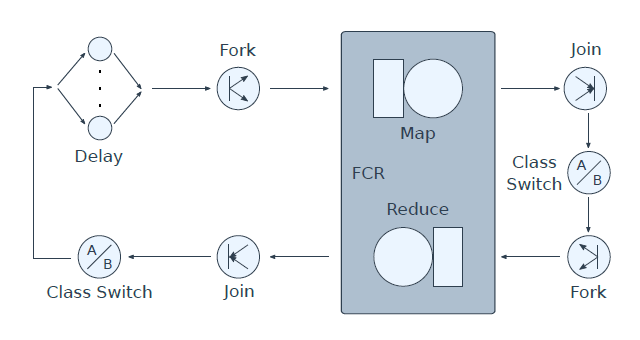
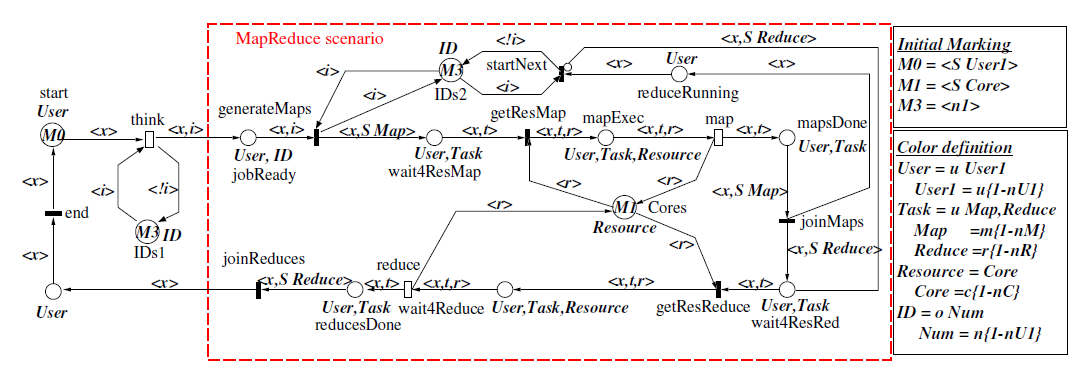
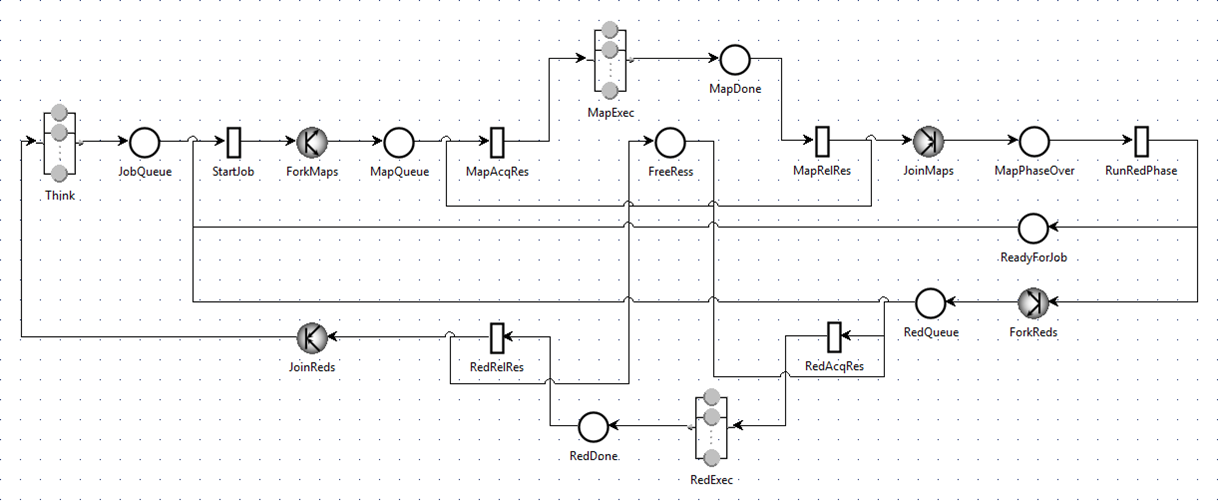
Within the scope of the DICE Project, we explored the use of hybrid models to analyze the performance of Big Data applications in an exact and concise manner, which can hardly be attained using either PNs or QNs if both logical and queueing behaviors are inherent in target systems. Consider performance analysis of the YARN capacity scheduler for example. The scheduler’s behavior is most simplified with a single class of job, and can be approximately and exactly captured by the QN and SWN (Stochastic Well-formed Net) models shown in Figure 1 and 2 respectively [3]. Figure 3 shows the hybrid model created with JSIM as an equivalent to the SWN model. In our context, we are particularly interested in the system throughput of the YARN capacity scheduler, i.e. the throughput at transition joinReduces in the SWN model and correspondingly that at join JoinReds in the hybrid model. The simulation results of the hybrid and SWN models collected by JSIM and GreatSPN [4] matched with each other. As the scale of the scheduler (e.g. the number of job classes) grows, merely a few number of components need to be added to the hybrid model whereas most substructures of the SWN model has to be duplicated multiple times.
Figure 1: The QN model of the YARN capacity scheduler with a single class of jobs.
Figure 2: The PN model of the YARN capacity scheduler with a single class of jobs.
Figure 3: The hybrid model of the YARN capacity scheduler with a single class of jobs.
As part of the PN extension, we also allow users to import/export PNML models with JSIM. PNML (Petri Net Markup Language) is a proposal of an XML-based interchange format for Petri nets [5, 6]. ISO/IEC 15909 (Systems and software engineering — High-level Petri nets) is dedicated to standardizing the PNML format. This standard consists of two parts: ISO/IEC 15909-1:2004+A1:2010 Part 1 formulates the concepts, definitions and graphical notation of Petri nets; ISO/IEC 15909-2:2011 Part 2 elaborates the specification of the transfer format on the basis of Part 1. Four types of PNML models are defined by the standard, namely core models, Place/Transition nets, symmetric nets and high-level Petri nets. In the current implementation, JSIM only supports import/export of core models and Place/Transition nets. The former are used to convey the topologies of PN models, while the later have been extended to represent GSPN models.
If you would like to know more about the JMT PN extension, full documentation can be found in both the JMT user manual and the DICE D3.4 deliverable.
Lulai Zhu, Imperial College London
References
- Marco Bertoli, Giuliano Casale, and Giuseppe Serazzi. JMT: performance engineering tools for system modeling. SIGMETRICS Perform. Eval. Rev., 36(4):10–15, 2009.
- F. Bause and P.S. Kritzinger. Stochastic Petri Nets: An Introduction to the Theory. Vieweg Verlag, 2002.
- Danilo Ardagna, Simona Bernardi, Eugenio Gianniti, Soroush Karimian Aliabadi, Diego Perez Palacin, and Jose Ignacio Requeno. Modeling Performance of Hadoop Applications: A Journey from Queueing Networks to Stochastic Well Formed Nets. In Proceedings of the 16th International Conference on Algorithms and Architectures for Parallel Processing, pages 599–613. Springer, 2016.
- G. Chiola, G. Franceschinis, R. Gaeta, and M. Ribaudo. GreatSPN 1.7: Graphical Editor and Analyzer for Timed and Stochastic Petri Nets. Performance Evaluation, special issue on Performance Modeling Tools, 24(1&2):47–68, November 1995.
- ISO. Systems and software engineering – High-level Petri nets – Part 1: Concepts, definitions and graphical notation. ISO/IEC 15909-1:2004+A1:2010, International Organization for Standardization, Geneva, Switzerland, 2010.
- ISO. Systems and software engineering – High-level Petri nets – Part 2: Transfer format. ISO/IEC 15909-2:2011, International Organization for Standardization, Geneva, Switzerland, 2011.

Sorry, the comment form is closed at this time.